La démarche scientifique

Version 3 du 31/12/98 par Jean-Michel Cornu. Cette création est mise à disposition sous un contrat Creative Commons (by-sa).

La science est un des moyens pour obtenir de la connaissance sur la réalité 4 étapes pour obtenir une connaissance scientifique L'observation La nouvelle Vision La mise en équations Les prévisions Le cycle scientifique Le cycle brisé Pour sortir de la crise

---

Ce texte présente les différentes étapes de la démarche scientifique. Il ne s’agit pas d’une vision absolue qui serait valable de tous temps, mais plutôt d’une analyse de la science telle qu’on la comprend aujourd’hui. Les étapes présentées s’appliquent plus particulièrement aux sciences fondamentales, mais peuvent servir de support à une réflexion sur les sciences de la nature et les sciences humaines. Ces dernières sont principalement basées sur l’observation, leur mathématisation étant plus empirique.

Je tiens à remercier le groupe Romani de l’Association pour la Création et la Diffusion Scientifique pour sa relecture attentive et ses remarques judicieuses qui ont grandement aidé à l’amélioration de la qualité de ce texte.

La science est un des moyens pour obtenir de la connaissance sur la réalité

La science et les autres démarches de connaissance

La démarche scientifique est un des moyens pour obtenir de nouvelles connaissances. Il est difficile de se faire une idée de la validité des autres façons d'obtenir de la connaissance (religions, etc.) en partant d'un point de vue scientifique car il s'agit de démarches différentes.

Tout se passe comme pour des personnes placées autour d'un objet et qui le regardent sous des angles variés. D'où ils sont, ils voient des choses différentes et parfois opposées (par exemple, la pièce vue entre deux personnes est-elle pile ou face ?).

Qu'est-ce que la réalité ?

Les différents moyens proposés par l'homme ont tous pour but de découvrir quelques pans de plus de la réalité. Ce que nous appelons les lois de la nature. Pourtant nous ne savons pas ce qu'est la réalité, si elle existe ou même si elle est unique.

Les succès de la science

La science moderne ne doit donc pas être vue comme l'unique moyen de découvrir la réalité. La démarche aristotélicienne qui prévalait en science avant le XVII^ème suivait un parcours différent des étapes présentées ici.

La démarche scientifique est cependant un moyen efficace qui a rencontré de grands succès. Un de ses intérêts majeur est de pouvoir faire des prévisions : Si d'une observation on tire une loi, et si on sait qu'un autre cas de figure est aussi soumis à cette même loi, alors on pourra prévoir son comportement avant même de l'avoir observé.

Par exemple, en connaissant la hauteur d'où est lancé un objet et l'accélération de la pesanteur, il est possible de prévoir la durée de sa chute.

Couvrir l'ensemble de la réalité ?

La science peut-elle traiter de l'intégralité de la connaissance ? Nous ne le savons pas, mais nous verrons plus loin que plusieurs aspects de la réalité nous semblent inaccessibles par la méthode scientifique.

---

4 étapes pour obtenir une connaissance scientifique

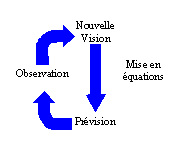
Les quatre étapes

La démarche scientifique a pour but de trouver les lois quantitatives qui produisent les phénomènes observés. Elle est constituée de quatre étapes :

1. L'observation
2. Une nouvelle vision
3. Sa mise en équations
4. Des prévisions observables

Le système reboucle ensuite pour observer si la prévision se réalise. Lorsque le cycle est complet, on peut alors considérer la loi proposée comme une vérité scientifique.

Le maillon le plus faible

Chacune des étapes comporte de nombreux pièges qui peuvent conduire à des erreurs scientifiques. De la même façon qu'une chaîne a la solidité de son maillon le plus faible, aucune des étapes ne doit être négligée.

---

L'observation

Observable et mesurable

En science, tout commence et tout finit par des observations. Les premiers pièges se situent ici. Tout est-il observable ?

Pour pouvoir mettre en équations les lois de la nature nous avons besoin non seulement d'observer mais également de mesurer. Tout est-il mesurable ?

Il nous semble aujourd'hui que plusieurs grandeurs ne sont pas observables ou mesurables et sortent donc du champ de la science telle que nous la décrivons ici.

Ce qu'il reste à observer

Pour les autres grandeurs, nous avons dans les siècles passés étudié une grande part de ce qui était facilement mesurable. Il reste au scientifique moderne a explorer les domaines qui sortent du champ immédiatement appréhendable par l'homme tels que l'infiniment petit, l'infiniment grand ou l'infiniment complexe.

Les statistiques au secours de l'observateur

Un autre cas de figure très courant en science est d'essayer de comprendre un phénomène très faible noyé dans d'autres données. C'est le cas lorsque l'on cherche à trouver une interaction entre certaines particules ou lorsque l'on veut comprendre un aspect des lois économiques dans un monde complexe.

Le scientifique se transforme alors en véritable détective pour retrouver une aiguille dans une botte de foin.

Une solution couramment utilisée est de réaliser un très grand nombre d'observations puis de faire une analyse statistique sur les résultats pour faire émerger l'élément observé et éliminer les autres phénomènes parasites.

L'action d'un médicament, par exemple, peut varier en fonction de beaucoup de facteurs. Il est donc nécessaire de tester un produit sur un grand nombre de sujets pour mieux le connaître avant de le commercialiser. On utilise même des groupes de sujets qui croient recevoir le médicament alors qu'on ne leur donne qu'une substance inactive (un placebo). Les statistiques sur les résultats entre les différentes populations permettent d'observer si les phénomènes psychologiques ne sont pas aussi fort que l'action chimique du produit lui-même !

Les phénomènes non reproductibles

Pourtant, si le recours à un grand nombre d'observation est souvent nécessaire, elle crée des difficultés nouvelles.

Certains phénomènes ne sont pas reproductibles à l'envie, et il faut les observer dans la nature lorsque celle-ci veut bien nous en gratifier.

Certains phénomènes astronomiques se produisent ainsi rarement et rendent complexe l'avancée des connaissances scientifiques.

C'est également le cas des aspects psychologiques qui sont très souvent non reproductibles et brouillés par d'autres phénomènes psychologiques.

De l'observation à l'expérimentation

L'observation se développe grâce à l'avancée des technologies. Celles-ci permettent d'explorer de nouveaux domaines. L'expérimentation peut reproduire autant de fois que nécessaire certains des phénomènes naturels.

L'expérimentation permet de passer d'une simple observation de phénomène naturel à l'observation mieux contrôlée des phénomènes provoqués par le scientifique.

Un excellent exemple du passage de l'observation à l'expérimentation est donné par l'étude des particules. Au début, le seul moyen d'observer de nouvelles particules était d'observer les rayons cosmiques. Aujourd'hui les accélérateurs de particules permettent de mettre en place des expérimentations qui favorisent l'observation de tel ou tel phénomène.

---

La nouvelle Vision

Changer notre vision du monde

L'étape suivante lorsque l'on a observé quelque chose qui ne rentre pas dans le cadre des lois connues est de changer son point de vue pour prendre en compte ces nouvelles données.

Très souvent il ne suffit pas d'étendre notre vision du monde. Il faut la changer complètement.

Le monde vu de la terre ou du soleil ?

Ainsi, Copernic à pris en compte les observations plus précises des trajectoires des planètes en étudiant leur déplacement non plus autour de la terre mais, autour du soleil.

Cette étape pourrait sembler facultative car il est possible d'obtenir des trajectoires justes en les calculant depuis la terre ou depuis le soleil. La différence est dans la complexité des équations qui régissent ces phénomènes.

Vu de la terre, les trajectoires devenaient de plus en plus compliquées au fur et à mesure que l'observation des planètes devenait de plus en plus précise. Il fallut imaginer des "roues dentées" supplémentaires pour faire fonctionner l'ensemble du mécanisme : Les épicycles.

Vu du soleil, au contraire, les trajectoires des planètes sont admirables de simplicité. Il s'agit de simples ellipses avec le soleil à l'un des foyers.

Retrouver les lois de la nature

Avoir une vision simple des choses comporte deux intérêts :

• Il devient plus facile d'en extraire une loi qui génère ce phénomène.
• Mais également, il devient plus facile de propager la connaissance.

Ainsi, Isaac Newton a-t-il pu déduire de la nouvelle vision du système solaire que les mécanismes célestes suivaient la même loi que les objets terrestres : Tous sont soumis à la gravitation qui est donc universelle.

Pour comprendre ce que cette vision avait de révolutionnaire, il faut savoir qu'à l'époque, le monde était séparé en deux parties soumises à des lois différentes :

• Sur terre, le mouvement de base est la ligne droite. Tout y est modifiable.
• Dans le ciel au contraire, le mouvement est basé sur le cercle et tout y est immuable

L'inspiration en science

L'outil que les scientifiques ont à leur disposition pour obtenir une nouvelle vision du monde est leur propre intuition.

Ceci explique les liens étroits que la science et les arts ont tissés par le passé. Léonard de Vinci a ainsi excellé dans la peinture comme dans les découvertes.

Tout comme n'importe quel art, la science nécessite d'allier l'inspiration et la maîtrise des outils. Si le musicien doit sans cesse faire des gammes, le scientifique doit continuellement parfaire ses qualités d'expérimentateur et ses connaissances mathématiques.

Il n'est pas nécessaire d'être sculpteur pour apprécier une sculpture, de même il est possible d'apprécier l'avancée des sciences sans en comprendre les mathématiques. Il est même possible qu'une nouvelle vision plus juste du monde sorte de l'inspiration d'un néophyte en matière d'expérimentation ou de mathématique. Cependant, pour être validée, cette nouvelle vision devra parcourir toutes les autres étapes du cycle scientifique. Notre néophyte devra alors convaincre des spécialistes de travailler à partir de sa propre vision, ce qui n'est certainement une chose aisée !

Comment avoir une "vision" ?

L'inspiration, l'imagination, et l'analogie avec d'autres phénomènes, guidés par l'intuition, sont les supports qui servent de base à une nouvelle vision du monde.

Le scientifique devra s'imprégner des nouvelles observations qui motivent le changement de vision afin d'imaginer un monde qui serait cohérent à la fois avec les expériences connues et avec les nouvelles observations.

Une des grandes difficultés dans ce genre d'exercice, est de s'abstraire de ses idées préconçues et de celles portées par son époque.

Ainsi, dans notre exemple précédent, Newton a imaginé une action a distance en contradiction avec les principes de son époque, aussi bien pour ce qui se passait sur terre que pour ce qui se déroulait dans le ciel. Il en conclut que dans les deux cas, les corps étaient attirés entre eux.

A la fin du XVII^ème siècle inspiré par les idées de Descartes, le monde était très mécaniste et refusait toute idée d'action à distance. Newton dut dépasser tous ces a priori pour énoncer ses lois.

---

La mise en équations

Tout ne se démontre pas

Cette nouvelle vision du monde va se traduire par de nouveaux postulats mathématiques. Ceux-ci sont le fondement de la théorie mathématique dont va découler toutes les équations qui décrivent le phénomène.

Il peut arriver cependant qu'une part de la théorie ne soit pas mathématisable, c'est à dire que certains aspects ne puissent être déduits des postulats de départ proposés. Dans ce cas, il est nécessaire d'ajouter aux équations des règles supplémentaires appelées principes, qui sont des constatations pour adapter les résultats aux observations. Les principes reflètent donc le caractère incomplet de la vision proposée pour décrire la réalité. Le principe de Fermat en optique, par exemple, "impose" à la lumière de prendre le chemin le plus court sans expliquer pourquoi.

Si la mise en équations mathématiques est un travail de déduction abstrait, les postulats et les principes sont eux issus de la vision proposée et de l'observation et permettent aux équations de "s'accrocher" au phénomène physique

Les mathématiques

Une fois une nouvelle loi identifiée, il est nécessaire de la formaliser pour en obtenir des informations quantitatives.

L'outil utilisé dans ce cas est la mathématique, ou plus exactement une des mathématiques. Il existe en effet de nombreuses façons de décrire un phénomène mathématiquement.

Ce fut le cas au début du XX^ème siècle, lorsque la mécanique quantique qui décrit le monde des particules élémentaires se développa. Dirac décrivit le comportement des particules à l'aide de l'algèbre des matrices, tandis que Schrödinger utilisa pour le même domaine les équations de champs. Il fallut de nombreuses disputes et des heures de travail ardu pour se rendre compte que les deux théories étaient équivalentes.

D'une mathématique à l'autre

Il est parfois extrêmement complexe de passer d'une mathématique à l'autre. Ceci explique la difficulté aujourd'hui de réunir plusieurs branches de la physique : La physique des particules utilise de nos jours les groupes de lie et les algèbres de Clifford alors que la relativité générale a opté pour l'algèbre tensorielle dans les variétés de dimension 4.

Il faut tout d'abord comprendre parfaitement plusieurs formes de mathématiques, ce qui revient à parler plusieurs langues. Mais il faut également être capable de transcrire une équation d'un formalisme dans un autre. Dans ce cas le problème peut devenir extrêmement complexe, voire quasiment impossible.

Le choix d'une mathématique

Le choix de la mathématique à utiliser pour décrire une loi de la nature n'est pas neutre. Suivant le cas, les équations ou les calculs peuvent être plus simples ou plus complexes. C'est le cas par exemple entre la trigonométrie et l'algèbre des nombres complexes.

Plus grave, le choix d'une mathématique, peut masquer un aspect du phénomène ou le rendre difficilement identifiable. On s'est ainsi rendu compte bien plus tard que l'électromagnétisme dont les lois ont été décrites au XIX^ème siècle par Maxwell en utilisant l'algèbre vectorielle, étaient relativistes avant l'heure !

Des dialogues de sourds

Cette multiplicité de possibilités pour mettre en équations le monde rend difficile le dialogue entre scientifiques de domaines différents.

Certain chercheurs isolés, suivent un chemin différent du gros des troupes. Leur escapade vers d'autres types de représentation peut ouvrir des voies prometteuses. La difficulté de dialogue entre les différentes "langues" mathématiques fait hélas que peu de personnes se penchent sur leurs travaux et qu'ils restent … isolés.

---

Les prévisions

Le monde passé à la moulinette

L'objectif d'avoir une théorie quantitative décrivant une loi de la nature est de la faire "mouliner" pour voir ce qui doit se passer dans divers cas de figure.

La théorie doit être cohérente avec les résultats antérieurs, aussi bien dans les cas traditionnels, que pour les nouvelles observations qui ont suscité une nouvelle théorie.

Mais cela ne suffit pas. Pour qu'une théorie soit acceptée, elle doit être capable de prédire des phénomènes non encore observés.

Einstein et les étoiles

Ainsi, une des conséquences étonnantes de la théorie de la relativité générale d'Einstein, était que la lumière était déviée par un corps massif. Une des façons de vérifier cela était de regarder si des étoiles situées dans le ciel à proximité du soleil avaient leurs rayons lumineux déviés par celui-ci. Elles seraient alors vues plus éloignées du soleil que prévu.

La seule façon d'observer ce phénomène à l'époque était d'attendre une éclipse totale du soleil afin que la luminosité de l'astre du jour ne gène pas l'observation des étoiles lointaines. Lors de l'éclipse suivante, les astronomes vérifièrent cette prévision de la théorie d'Einstein. Ce fut une confirmation éclatante de ses hypothèses.

L'outil de la prévision

De plus en plus souvent, les théories doivent prévoir des phénomènes extrêmement subtils ou nécessitant des moyens supérieurs à ce que la technologie sait réaliser pour proposer des observations non encore réalisées. Pour réaliser ces prévisions, un des outils principaux est le calcul numérique. Les ordinateurs y sont dans leur élément et facilitent de nos jours grandement cette étape.

Les mathématiques permettent de définir des lois quantitatives. Le calcul numérique lui, "mouline" ces lois à partir de conditions initiales.

Prévoir puis observer pour démontrer

Le résultat de ce calcul est alors ce que l'on cherche à observer en provoquant les mêmes conditions initiales dans une expérimentation.

Les théories dites de "grande unification" cherchent à réunir les deux grands résultats du XX^ème siècle : La physique des particules et la relativité générale. Ces diverses théories prévoient différentes nouvelles particules ou des comportements nouveaux. Les expérimentateurs recherchent dans les anneaux de collision, comme au CERN ou bien dans d'immenses piscines enterrées sous les montagnes, la vérification de ces théories.

---

Le cycle scientifique

La boucle est bouclée

Une fois que la nouvelle théorie a permis de faire des prévisions, la dernière étape est donc d'observer ou de réaliser des expérimentations pour les confirmer ou les infirmer.

La boucle est bouclée et nous sommes de retour à l'étape de l'observation.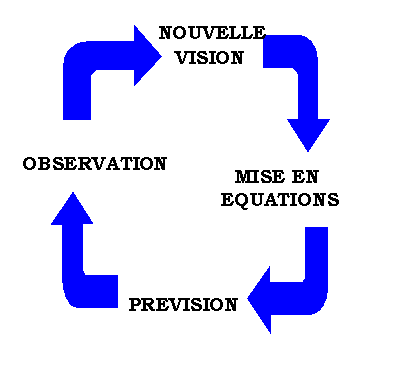

En fait, le point d'arrivée n'est pas tout à fait le point de départ. De la même façon, lorsque la grande aiguille d'une horloge à fait un tour complet, une heure de plus s'est écoulée. Le cycle de la science ressemble plus à une spirale qu'à un cercle classique : A chaque tour, au cours du temps, nos connaissances sur la nature se sont développées.

Il ne reste plus qu'à entamer un nouveau tour dans un mouvement sans fin de l'humanité vers la recherche de la connaissance.

Une hypothèse, c'est vrai ou c'est faux ?

Dans notre monde encore très emprunt de manichéisme, une chose doit être vraie ou fausse. Pourtant en science, une théorie n'est ni vraie ni fausse tant qu'elle n'a pas parcouru l'ensemble du cycle. Il s'agit d'une hypothèse. Même une fois démontrée à l'aide des différentes étapes de la démarche, on ne peut être sûr qu'une théorie sera vraie à 100%.

Erreurs et approximations

Tout d'abord, il peut y avoir des erreurs de mesure ou d'interprétation. En expérimentation, en particulier lorsque l'on utilise un grand nombre d'expériences, on considère qu'un phénomène est certain au sens des probabilités lorsqu'il y a moins d'une chance sur 100000 ou sur 1 million que le résultat soit du au hasard. Il n’existe donc pas de preuve absolue.

Par ailleurs, il ne faut pas confondre la carte et le territoire. La théorie n'est que la meilleure représentation possible de la réalité à un moment donné. Elle ne s'applique que dans des limites données. Ainsi la relativité d'Einstein, n'a pas infirmé les lois de la gravitation de Newton mais les a complétées et étendues au domaine des grandes vitesses et des grandes masses.

Le chercheur coincé entre les convaincus

De tout temps, le chercheur a du naviguer sur la frontière étroite de la recherche. Il doit faire face à ceux qui considèrent que sa théorie ou ses observations sont fausses comme à ceux qui les considèrent a priori comme juste.

Parfois, la recherche touche des points qui ont une influence politique (les races humaines), éthique (les manipulations génétiques), religieuse (la place de la terre dans l'univers) ou jouent sur les peurs et les désirs de l'homme (les possibilités du cerveau ou de l'esprit humain). Dans ce cas, il est plus difficile encore d'étudier sereinement une hypothèse.

De plus, lorsque le champ d'observation est mal mesurable, peu reproductible et difficiles à isoler, comme dans le cas des aspects psychologiques, la recherche scientifique cumule les difficultés.

---

Le cycle brisé

Outre les difficultés expérimentales, les pièges mathématiques, et les pressions de l'environnement politique et culturel, il existe une façon courante de dénaturer la démarche scientifique : Très souvent, des étapes du cycle sont omises.

Quelques exemples nous permettent de comprendre les difficultés rencontrées par la science. Il faut prendre ceux-ci comme des tendances permettant de mieux comprendre les problèmes de la science, plutôt que comme des caricatures.

La science aristotélicienne

Avant le XVII^ème siècle, la démarche scientifique était moins complète. Le chaînon manquant était … l'observation ! Il n'était alors pas nécessaire de vérifier une théorie par l'observation ou l'expérimentation.

Les Grecs ont fait des avancées majeures en science. L'osmose entre la philosophie et les sciences a été une façon très féconde de développer une vision du monde. Le sens de la déduction et le haut niveau mathématique des pythagoriciens a permis une mise en équations poussée en particulier dans le domaine de la géométrie. Cependant les prévisions réalisées par la théorie n'étaient pas mises à l'épreuve de la réalité.

Pourtant, la science grecque a remporté de nombreux succès, en particulier en imaginant l'atome et le déplacement des planètes autour du soleil. Mais le manque de vérification des hypothèses ne permettait pas de choisir entre les théories concurrentes et tout était une question de confiance et d'autorité.

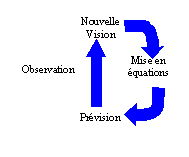Le moyen âge a hérité de cette démarche. L'astronomie fut une exception notoire. Elle était principalement destinée à prévoir l'emplacement des astres et des planètes, ainsi que la date des éclipses.

Il fallut attendre pour voir évoluer les choses la fondation de la Royal Society en 1660 en Angleterre avec Boyle et Newton et en France l'arrivée de Descartes puis de l'Académie des sciences en 1666 avec en particulier le Néerlandais Huygens. Depuis, lorsqu'il n'est pas possible de vérifier une théorie par l'observation directe (par exemple pour les particules élémentaires), on utilise les conséquences des équations mathématiques de la théorie pour faire des prévisions observables (comme la trace du passage d'une particule dans une chambre à bulle).

Les pseudo-sciences

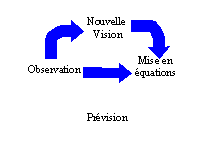La recherche d'une nouvelle vision de l'univers est plaisante et enivrante. Lorsqu'une personne dispose d'une culture scientifique, elle est vite tentée par cet exercice. C'est une très bonne chose car, comme nous l'avons dit, il est possible qu'une vision plus juste vienne d'un non-spécialiste moins gêné par les a priori. Cependant, il existe une erreur extrêmement fréquente chez ceux qui s'essayent à la science : Ils omettent d'imaginer des prévisions observables de leur théorie.

Dans ce cas, le candidat chercheur utilise des observations non encore expliquées par la science et donne sa vision des faits au travers d'une hypothèse.

Mais cela n'est pas suffisant pour prouver une théorie. Il faut que celle-ci puisse prévoir des faits non encore observés. A défaut, la théorie restera au niveau de l'hypothèse : ni vraie, ni fausse.

Les épicycles

Plusieurs fois dans l'histoire de l'humanité, des brances de la science se sont retrouvées en panne. Les théories se compliquaient au fur et à mesure des progrès obtenus dans l'observation.

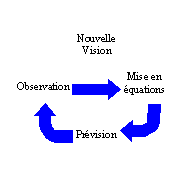L'astronomie au XIV^ème siècle en est un bon exemple. Celle-ci était performante pour faire des prévisions, contrairement à la science aristotélicienne de l'époque. Pourtant, au fur et à mesure que les instruments d'observation devenaient plus puissants, il fallut corriger les trajectoires des planètes en plaçant dans leur mécanisme de déplacement quelques "roues dentées" supplémentaires appelées les épicycles. L'harmonie parfaite du mouvement circulaire céleste était ébranlée.

Les équations des trajectoires devenaient de plus en plus complexes. De fait, le mouvement des planètes vus de la terre n'est pas simple : Mars a le mauvais goût de revenir parfois en arrière, quant à Mercure et Vénus, elles ne font même pas le tour complet de la terre. Il fallut que Copernic et Kepler se penchent sur ce problème pour que l'on se rende compte que les choses sont bien plus simples vues du soleil que vues de la terre.

Il faut bien comprendre que les trajectoires des planètes vues de la terre ne sont pas fausses pour autant. Il est possible de déterminer le mouvement d'un corps à partir de n'importe quel repère, y compris la terre. Cependant, la vision du mouvement à partir de la terre est très nettement plus complexe que celle obtenu en prenant le soleil comme point de repère. Cela est du au fait que la loi qui gouverne la marche des planètes est basée sur une interaction entre celles-ci et le soleil : La gravitation.

Le rasoir d'Occam

Il semble qu'il soit toujours possible de trouver une vision assez simple des faits observés. C'est même une règle qui permet dans une première approche de choisir entre deux visions du monde.

Guillaume d'Occam (ou Ockham) était un franciscain anglais vivant au XIV^ème siècle. Il proposa un principe de base "Pluralitas non est ponenda sine neccesitate" (les entités ne doivent pas être multipliées inutilement). Cela peut se traduire pour le scientifique de la façon suivante : Si vous avez deux théories concurrentes qui amènent exactement les mêmes prévisions, la plus simple est la meilleure.

Les coups de rasoir supprimant les éléments non nécessaires et non observables ont été un moyen puissant de choisir entre deux visions du monde la mieux adapté.

Ce principe du rasoir d'Occam doit cependant rester un outil dédié à l'étape du cycle destinée à obtenir une nouvelle vision et ne remet pas en cause les façons d'opérer les autres étapes. Il ne faut pas aller aussi loin qu'Aristote, qui proposait un principe équivalent : "La nature fonctionne de la plus courte façon possible". Il en déduisit que ce simple principe était suffisant pour démontrer une théorie et que l'observation et l'expérimentation étaient inutiles.

De plus, il faut manier le rasoir avec précaution : si la nature semble choisir la solution la plus simple, elle est également pleine de pièges en trompe l'œil…

La science du XX^ème siècle

Le XX^ème siècle aura vu une nouvelle fois la science fondamentale en panne et la complexité envahir les théories. Pourtant, tout avait bien commencé.

Le XIX^ème siècle avait pratiquement parachevé la mécanique et les équations de Maxwell unifiaient l'électricité, le magnétisme et l'optique. On pensait même à cette époque que les scientifiques du XX^ème siècle s'ennuieraient, tout ayant été trouvé ou presque !

Le début du siècle a pourtant vu deux révolutions majeures dans les sciences :

• La relativité restreinte puis générale d'Einstein, décrit ce qui se passe lorsque la vitesse d'un corps approche celle de la lumière, ou lorsque sa masse est grande. Elle donna le jour à la cosmologie, l'étude de l'univers dans son ensemble.
• La mécanique quantique puis la physique des particules étudient le monde des très petites dimensions, celui où vivent les particules.

Parallèlement, ce siècle à vu le développement d'un formidable progrès technologique qui a permis de construire des outils d'observation toujours plus puissants.

Petit à petit, les équations de la mécanique quantique ont été adaptées aux nouvelles observations sans changer radicalement notre point de vue. La situation est proche de celle qui prévalait à l'époque des épicycles : Les équations deviennent de plus en plus complexe et masquent le sens physique des faits observés. La physique des particules est arrivé à un très haut degré d'abstraction : La théorie des groupes permet d'imaginer toutes les symétries possibles dans tous les types d'univers. Il s'agit alors de trouver les symétries qui correspondent à la réalité observée pour chaque type de particule et de force. Pour réunir toutes les forces, et particulièrement la gravitation qui résiste à cette analyse, les scientifiques recherchent une super-symétrie qui prenne en compte la physique des particules et la relativité.

Une science fondamentale compliquée mais efficace

Ce manque de nouvelle vision ne veut pas dire que les théories soient fausses ou qu'elles ne permettent pas de faire des prévisions. Bien au contraire, la physique des particules a remporté de très nombreux succès en prévoyant le comportement des particules dans des conditions particulières ou en en découvrant de nouvelles. Mais la théorie devient complexe, avec de nombreuses ramifications que le rasoir d'Occam n'a pu couper, faute de pouvoir la remplacer par une vision plus simple. Le XX^ème siècle cherche ses Copernic, Tycho Brahe, Kepler, Galilée ou Newton pour retrouver une vision simple.

L'apparition des paradoxes

Lorsque l'on introduit dans une ancienne théorie un nouvel élément pour lequel elle ne s'applique pas, il se manifeste un phénomène curieux : l'apparition de paradoxes. La science moderne en est remplie.

Un exemple bien connu est l'apparition de valeurs infinies dans les équations. Il faut bien souvent "torturer" les équations pour leur redonner des valeurs plus acceptables. Le processus appelé renormalisation rentre dans ce cadre. Il permet, au prix d'un artifice mathématique, d'éviter qu'une grandeur ne soit infinie à un point donné. Le plus étonnant est qu'il donne des résultats justes sans que personne ne comprenne pourquoi !

L'exemple de l'hôtel infini

Un exemple de paradoxe est donné par l'hôtel infini. Celui-ci comporte une infinité de chambres qui sont toutes occupées. Lorsqu'un nouveau client arrive, celui-ci est donc complet. L'aubergiste cependant a trouvé une astuce pour accueillir le nouvel arrivant : Il demande à l'occupant de la première chambre de déménager pour laisser la place au nouveau client et de s'installer dans la chambre numéro 2. Bien sûr, l'occupant de la chambre n°2 doit lui aussi déménager et il ira s'installer dans la chambre n°3. Ainsi de suite, les occupants s'installent chacun dans la chambre suivante. Comme il y a un nombre infini de chambre, aucun client n'est laissé à la porte car il pourra toujours trouver une chambre suivante.

Dans ce cas, nous avons utilisé les lois de l'addition dans un domaine où elles ne s'appliquent plus : L'infini plus un est toujours égal à l'infini !

Il ne suffit pas d'étendre les anciennes théories pour y ajouter les faits nouveaux découverts. Parfois, il est indispensable de changer notre vision du monde pour que les nouveaux faits puissent s'y appliquer.

Les sciences de la nature

En ce qui concerne les sciences de la nature, l’approche est différente. L’observation est particulièrement développée. Des théories prometteuses ont proposées des visions efficaces qui ont permis de faire des prévisions confirmées par de nouvelles observation. C’est le cas de la géologie et de la géomorphologie par exemple qui ont pu être appliquées à l’études des autres planètes du système solaire.

La mise en équation mathématique est cependant plus empirique dans les sciences de la nature. S’il est souvent possible d’obtenir des informations quantitatives, celle-ci sont basées sur des principes plutôt que sur des lois fondamentales.

---

Pour sortir de la crise

La difficulté que rencontrent les scientifiques du XX^ème siècle à trouver une théorie qui unifie la mécanique quantique et la relativité ; l’aspect compliqué des hypothèses actuelles ; l'émergence de nombreux paradoxes dans les théories ;

Tout indique que la science actuelle traverse une crise et que le cycle de la démarche scientifique est déséquilibré.

• L'observation a fait des progrès fantastiques grâce à l'arrivée de technologies toujours plus performantes
• Les prévisions issues des théories bénéficient du formidable essor de l'informatique.

Sur ces deux points, il s'agit simplement de continuer avec toujours plus de rigueur et d'efficience.

Par contre, il est indispensable de développer nos outils pour obtenir de nouvelles visions et des représentations mathématiques performantes.

Comparer et choisir les mathématiques

Pour ce qui est de la mise en équations, il faut faciliter la comparaison entre des théories exprimées dans des formalismes différents.

Il est important d'avoir une meilleure vision d'ensemble des différentes mathématiques et de leurs liens, pour faciliter le choix du formalisme le plus pertinent.

Des outils pour une nouvelle vision

Le verrou principal du développement de la connaissance scientifique est le manque de vision nouvelle. Nous avons défini quelques outils qui doivent être développés et utilisés :

• L'intuition
• L'imagination
• L'inspiration
• L'analogie avec en particulier ses deux formes décrites par Lucien Romani (l'amalgame et l'analyse parallèle)
• Le rasoir d'Occam permet une première sélection parmi les différents candidats.

S'abstraire de l'environnement

Enfin, et c'est sans doute une des choses les plus difficiles, il est nécessaire de s'abstraire des contraintes de notre environnement (physique, culturel, politique…) pour éviter d'ajouter des contraintes supplémentaires aux théories.

Le cycle scientifique décrit ici est lui-même inscrit dans le temps. Il est plus complet comme nous l'avons vu, que la démarche scientifique aristotélicienne d'avant le XVII^ème siècle. La science des siècles futurs sera probablement encore différente.

L'art et la science sont frère et sœur. Il est temps de retrouver l'inspiration, sans renoncer à la rigueur. La connaissance scientifique demande de la belle ouvrage.

---